 Frigidus Symmetria
Frigidus Symmetria

Lex Ⅲ:Reactio(反作用)
私の部屋には、沢山の本や書類が所狭しと並んでいる。元々、本は沢山あった。
それに加え、今回の調査のために沢山の資料を取り寄せたのだから、山積みとなるのは当然の帰結だ。
元々ある本の中には、『原論』、『プリンキピア』、『プリンキピア・マテマティカ』、
『解析力学』、『天体力学』等の数学、物理学関係が多い。
あなたが好きで、私によく教えてくれたからだ。私も、その影響からかそれらが好きになった。
逆に、歴史や文学、芸術等はその曖昧さに腹を立てていた。対称性や黄金比など数学的要素を持った作品は好きだったが。
Sequere Naturam
自然に従え
昔は、その言葉に非常に共感していた。だが今は……
山積みの本の中から一冊の本を引き出す。
不安定な平衡点にあった本の山が崩れだす。まるで地震のように。
無作為に本のページを開く。
それは、ユークリッドの『原論』の公準が記された箇所だった。
ふいに、第五公準が目に入った。第五公準、平行線が交わらないという公準は、他の公準に比べ、自明ではなかった。
それ故、この公準が必要なのかを考える者が多々あった。
そして、この第五公準が不要になった時、非ユークリッド幾何学が生じた。
それは相対論にも用いられ、重力は四次元時空の歪みとして表された。
ユークリッド幾何学は崩壊した。だが、代わりに作られたのは何か?
光速度不変の原理。質量を持つ存在は決して光に追いつけない。アキレスと亀のパラドックスが成立する。
次に取ったのは『プリンキピア』だった。物理学の聖典ともいえる書物だ。
ニュートン力学は知っていたが、私が教わったのはオイラー等によって数式化されたものだ。
この本は微分積分という代数的方法を用いずに、全て幾何学で書かれている。
ニュートン、ライプニッツによって微積分が作られたのにもかかわらず。形式も『原論』を踏襲している。
そして、
ニュートンの運動の三法則(Axiomata Sive Leges Motus)
これがあなたを殺した法則だ。
ニュートンは、自分が発見した知識についてこう語った。
「私は、広い浜辺で綺麗な石を見つけて喜んでいる子供に過ぎない」
私はこう言おう。
「私は広い浜辺で、とても小さいが大切な石を失くした。
それを何日も一人で探して見つからず……
誰かに手伝ってもらっても見つからず……
シャベルカーで掘削しても見つからなくて……
気付けば、要らない砂にまみれていた老人に過ぎない」
数多の本。そこには当然ながら数式が並んでいる。
この数式があなたの生命を奪ったのだ。数式には様々な記号がある。
一番使われているのは”=”(等号)だ。
”=”が憎い。
私は、なぜ科学を学んできたのだろう? あれほど、好きだった数学と物理学とが今では、一番嫌いだ。
『原論』を『プリンキピア』を、数式の書かれた本を破いて、破いて切り裂いた。
本だけではない。頭の中にある覚えてしまった無数の数式が、全ての知識が嫌になる。
全てを疑え。それが科学の真髄ではなかったのか?
そうだ。全てを疑い、吟味した。オッカムの剃刀で切り裂いた。可能性を探し続けた。
全てを疑っても残るものがある。
事実と私自身だ。私は存在しないと考えようとすれば、私が存在する。
Cogito ergo sum
我思ふ 故に我あり
客観的事実は、かなり妥当性がある。けれども、疑う事もできる。
だがそうしたらあなたの存在すら消してしまう。それは出来ない。
あなたが教えてくれた数式を、知識を全て忘却したいが、あなたの事は忘れたくない。
ニュートンのゆりかごが目に入る。
片方の球が並んだ球に当たり、反対側の球を弾く。ただ、その運動を繰り返す。
静寂に近いこの部屋でも球の衝突音はしない。
その理由は、昔、あなたと共に完璧な物を目指したからだ。
その特別なゆりかごは、空気抵抗をなくす為、内部を真空にし、その球は非弾性衝突を避けるために、特殊な素材で作り、反発係数eをほとんど1に近づけてある。
なので普通のものと比べて、長時間、運動を繰り返す。
コルプスが生きていた時から、減衰せず運動量保存則に支配されていた。
あなたの生死など何の影響もないと嘲笑している様だった。
それを否定したくて、机から叩き落した。
ゆりかごは放物線を描いて落ちていき、ようやく運動を止めた。
ゆりかごの静止と同時に、ゆりかごではない何かが割れる音がした。
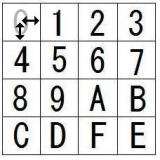
ゆりかごの下には、壊れて歪んだ15パズルがあった。
その15パズルはコルプスの手作りで、1~15までの数字の代わりに、16進数表記が使われていた。
つまり、1~9とA~Fまでだ。そしてFとEの配置だけが逆になっていた。
あなたはそれを、十進数の16に相当するFから、”Fパズル”と名付けていた。
昔、あなたが私にこれを渡して解かせたのだった。
私は疑問に思って尋ねた。
「Fパズルといったって、ただの15パズルじゃないですか。何故これを解かせるんですか?」
あなたは面白そうに答えた。
「ただのパズルと侮るなかれ。数学的に考えればきっと答えが出るはずさ」
私はFパズルを解き始めた。これまでに何度か15パズルはやっていたから、いつもの様に感覚で、マスを揃えようとした。
しかし数時間やっても解けなかった。私はあなたの助言通り、数学的に考え始めた。
そういえば、マスの動かし方には規則性がある。それを数学で表現できるはずだ。
おそらく、数学の本などに、問題の答えは載っているだろうが、それを見る事は卑怯だと思い、私は独力で頑張った。
その問題はとても難しかった。規則性に気付いて、答えに近づいたと思うのだが、何故か問題は解けなかった。
解けないはずがないのに……
ついに私は諦めて、あなたに答えを聞いたのだった。
あなたは群論を用いて、証明を始めた。私が独力で考えていた概念に近かったが、更に洗練されていた。
そして、証明の答えは”解けない”、つまりFake(偽物の)パズルだった。
そんな問題を出すあなたに少し腹が立った。私の努力は無意味だったからだ。
私の怒りに気付いたあなたは弁解とも開き直りとも解釈できる事を言った。
「アクアの悩んだ時間など、数学者達が、五次以上の代数方程式が解けない事を証明するのに費やした年月に比べれば短いものさ」
その時の私は、怒りよりも好奇心が大きかったので、あなたからその歴史を聞く事にした。
この問題を通して、方程式の解法や群論の歴史など、あなたから得たものも多かったが、好奇心が少し満たされると、解けない問題をやらされた不満が再び戻ってきた。
だから後日、家をとりまく環(Ring)状に落とし穴を地面(Field)に掘り、仕返しをした。
私は高いポテンシャルから、低ポテンシャルにいるあなたを見て笑った。あなたも驚いたが、つられて笑った。
あの時は二人とも笑っていたのに、低ポテンシャル(深海)に落ちたあなたも、高ポテンシャル(水面)に浮かんだ私も、今はもう笑う事が出来ない。
過去に浸ろうと、Fパズルのマスを動かそうとしたが、先ほどの衝撃で歪み、動かなかった。
動いても動かなくても、どちらにしても解けない事に少しして気付いた。
近くには、プラトンの5つの正多面体、つまり、正4、6、8、12、20面体が飾られている。
どの立体も鏡像対称性、回転対称性など様々な対称性(Symmetria)を有している。
私は対称という言葉を知る前から、左右が同じ形状のものを好み、そうでないものには嫌悪感を抱いた。
成長してからも私には非対称なものは合理(Ratio)的ではないと思えた。
私は、透明な正20面体を手に取った。

表面にはいくつかの点と記号が書かれていた。
それは、Fパズル事件が終わり、私が群論を勉強し始めた時に、あなたが説明のために書いた回転対称軸の印だった。
あなたは、クラインの『正20面体と5次方程式』やワイルの『シンメトリー』等と共に正多面体を用いて、
群論が代数方程式だけでなく、正多面体にも応用できる事や正20面体と5次方程式の可解群が同じ事を嬉しそうに説明した。
更に、あなたはネーターの定理など、物理法則と対称性の関係を話し、それらが成す美を教えてくれた。
その時の私は、あなたの高度な説明をまだあまり理解できなかったが、対称性の美しさは理解できた。
特にワイルの『シンメトリー』に引用された詩は印象的だった。
God, Thou great symmetry
神々しき、汝、大いなる対称性よ
Who put a biting lust in me
汝は痛切な望みに我を掻き立てる
From whence my sorrows spring,
我が悲しみの泉より
For all the frittered days
空しく過ぎ去りし全ての日々
That I have spent in shapeless ways
形無く彷徨ったその日々に
Give me one perfect thing.
汝は、我に完全な存在を知らしめる
Anna Wickham 『Envoi』
何度、この詩を口ずさんだ事だろう?
だが今は、”=”と同様にそれが憎い。否、”=”はその一部だから、真に憎むべきは対称性(Symmetria)だ。
私は、持っていた正二十面体を回転させた。
しかし、360度回転させる前に、何度も同じ形に戻った。
ここにも対称性があった。それも記されたいくつかの点を軸にして回す限り、いつも元に戻った。
[c,C] = 0
(物質(corpus)とコルプス(Corpus)の交換は対称)
まるでそう主張しているようで、憎くなった。
透明な正二十面体、プラトンの”水(aqua)”を地面に叩き付けた。
Frigidus Symmetria(冷たい対称性)は破れ、ビッグバンの如く欠片が無秩序に飛び散った。
 Frigidus Symmetria
Frigidus Symmetria



